
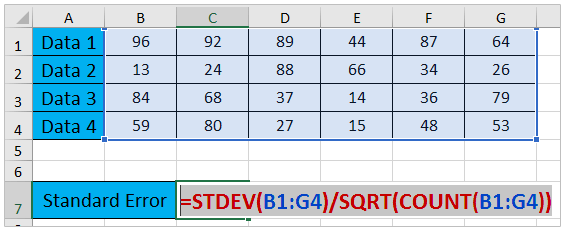
#HOW TO CALCULATE STANDARD ERROR WITHOUT STANDARD DEVIATION HOW TO#
How to interpret the residual standard deviation/error
Now that we have a statistic that measures the goodness of fit of a linear model, next we will discuss how to interpret it in practice. The degrees of freedom df is equal to the sample size minus the number of parameters we’re trying to estimate.įor example, if we’re estimating 2 parameters β 0 and β 1 as in: The simplest way to quantify how far the data points are from the regression line, is to calculate the average distance from this line: Residual standard deviation vs residual standard error vs RMSE Now that we developed a basic intuition, next we will try to come up with a statistic that quantifies this goodness of fit. Mathematically, the error of the i th point on the x-axis is given by the equation: (Y i – Ŷ i), which is the difference between the true value of Y (Y i) and the value predicted by the linear model (Ŷ i) - this difference determines the length of the gray vertical lines in the plots above. In the plots above, the gray vertical lines represent the error terms - the difference between the model and the true value of Y. Therefore, using a linear regression model to approximate the true values of these points will yield smaller errors than “example 1”. This is because in “example 2” the points are closer to the regression line.

Just by looking at these plots we can say that the linear regression model in “example 2” fits the data better than that of “example 1”.


 0 kommentar(er)
0 kommentar(er)
